Physics AS- Waves

4.1 WAVES AND VIBRATIONS

Types of waves:

Waves that pass through a substance are vibrations which pass through that substance.
Sound waves in air are created by making a surface vibrate so it sends compression waves through the surrounding air.
Sound waves, seismic waves and waves on strings are known as mechanical waves.

Longitudinal waves:

Waves in which the direction of the vibrating particles is parallel to the direction in which the wave travels.
e.g.: Slinky
When one end of the slinky is moved to and fro repeatedly, each forward movement causes a compression wave to pass along the slinky as each coil pushes another.

Transverse waves:

Waves in which the direction of vibration is perpendicular to the direction in which the wave travels.

Electromagnetic waves:

Oscillating electric and magnetic fields that progress through space without the need for a substance to travel through.
Vibrating electric field generates a vibrating magnetic field, which also generates a vibrating electric field further away.

Polarisation:

Transverse waves are plane-polarised if the vibrations stay in one plane only.
If the vibrations change from one plane to another, the waves are un-polarised.
Longitudinal waves CANNOT be polarised.
Light from a filament lamp is un polarised, if it passes through a Polaroid filter, the transmitted light becomes polarised as the filter only allows through light which vibrates in a certain direction.
If un polarised light is passed through two Polaroid filters, the transmitted light intensity changes if one Polaroid is turned relative to the other one.
The filters are said to be crossed when the transmitted intensity is a minimum, At this position, the polarised light from the first filter cannot pass through the second filter.

Using this diagram, the wave passes through the first fence due to the position of the slit in the fence. But through the second fence, it is rotated 90° and therefore the wave cannot pass through due to the alignment.

4.2 MEASURING WAVES:

Displacement: of a vibrating particle is its distance and direction from its equilibrium position.
Amplitude of a wave is the maximum displacement of a vibrating particle. For a transverse wave, this is the height of crest of the depth of a wave trough from its equilibrium position.
Wavelength of wave is the least distance between two adjacent vibrating particles with the same displacement and velocity at the same time.
One complete cycle of a wave is from maximum displacement to the next maximum displacement. e.g: One trough to another.
Period of a wave is the time for one complete wave to pass a point.
The frequency of a wave is the number of cycle of vibrations or particles per second. or the number of complete cycles passing a point per second. (Hz)

For the the period of a wave: 1/f

Wave speed:

Higher the frequency, the shorter the wavelength
For example: if waves are sent along a rope, the higher the frequency at which they are produced, the closer the wave peaks are.

∴ The Speed of the waves, c=Distance travelled in one cycle/time taken for one cycle

∴ = λ/1/f =f λ

∴ Wave speed c=fλ

Phase difference:

For two points at distance d apart along a wave of wavelength λ:

PHASE DIFFERENCE= 2ΠD/Λ

For phase difference questions: make sure to understand the distance from a fixed point, in this example, it’s from the point ‘O’ and then you can sub it into the phase difference formula to answer the question. Be careful with these types of questions as it’s easy to make mistakes with radians if you aren’t careful or prepared.

4.3 WAVE PROPERTIES

A ripple tank may be used to show wave properties such as reflection, refraction and diffraction.
The waves observed in a ripple tank are referred to as “wave-fronts” which are lines of constant phase.
The direction in which waves travel at are at right angles to the wave-fronts.

Reflection:

Straight waves directed at a certain angle to a hard flat surface (reflector) reflect off at the same angle.

Reflection of plane waves
The angle between the reflected wave front and the surface is the same as the angle between the incident wave front and the surface.

Refraction:

When waves pass across a boundary at which the wave speed changes, the wavelength also changes.
IF the wave fronts approach at an angle to the boundary, they change direction as well as changing speed.
Changing speed and direction = refraction
An example of refraction is shown when water passes a boundary of shallow to deep water at angle to the boundary. Because they move slower in the shallow water, the wavelength is slower in the shallow water and therefore it changes direction.
Also shown when light is directed at a glass block at an angle, therefore not along the normal.
The light ray changes direction when it crosses the glass boundary due to light travelling slower in glass than in air.
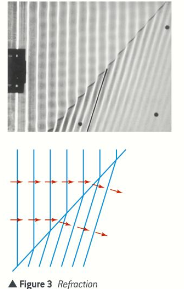
Refraction

Diffraction:

Occurs when waves spread out after passing through a gap or round an obstacle.
Effect can be seen in a ripple tank when straight waves are directed at a gap.
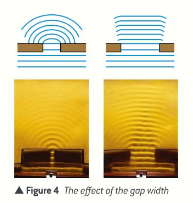
The narrower the gaps, the more spread out the waves are.
The longer the wavelength, the more spread out the waves are.

Dish design:

Satellite dish’s in Europe need to face the south due to the satellites orbiting the Earth directly above the equator.
The bigger the dish, the stronger the signal it can receive because more radio waves can be reflected by the dish onto the aerial.
However a bigger dish also reflects the radio waves to a smaller focus because it diffracts the waves less. The dish therefore needs to be aligned more carefully than a smaller dish

4.4 WAVE PROPERTIES 2

Principles of superposition:

The principle of superposition states that when two waves meet, the total displacement at a point is equal to the sum of the individual displacements at that point.

When a crest meets a crest, a super-crest is created (the two waves reinforce each other)
When a trough meets a trough, a super-trough is created (the two waves reinforce each other)
When a crest meets a trough of the same amplitude, the resultant displacement is Zero. the two waves cancel each other out.

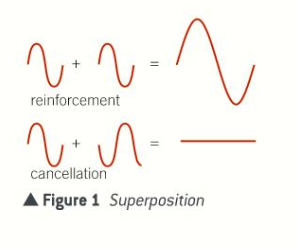
Examples of superposition:

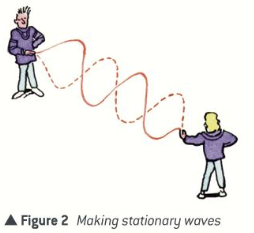
Stationary waves on a rope

Stationary waves are formed on a rope if two people send waves continuously along a rope from either end. The two sets of waves are referred to as progressive waves to distinguish them form stationary waves.
They combine at fixed points along the rope to form points of no displacement or nodes along the rope.
At each node, the two waves are always 180° out of phase, so they cancel each other out.

2. Water waves in a ripple tank

Points of cancellation are created where a crest from one dipper meets a trough from the other dipper. These points of cancellation are seen as gaps in the wave-fronts.
Points of reinforcement are created where a crest from one dipper meets a crest from the other dipper, or a trough from one dipper meeting another trough from another dipper.
As the waves are continuously passing through each other at a constant frequency and a constant phase difference, cancellation and reinforcement occurs at fixed positions.
This effect is called interference. Coherent sources of waves produce an interference pattern where they overlap, because they vibrate at the same frequency with a constant phase difference.
If the phase difference changed at random, the points of cancellation and reinforcement would move at random, and no interference pattern would be observed.

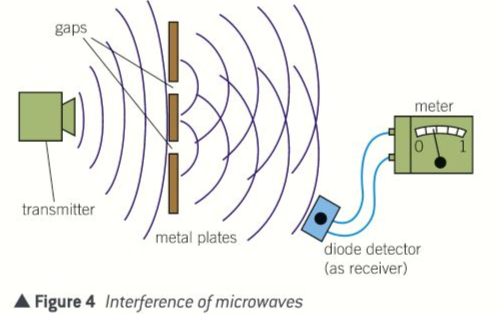
Tests using microwaves:

Place the receiver in the path of the microwave beam from transmitter.
Move the receiver gradually away from the transmitter and note that the receiver signal decreases with increased distance from the transmitter.
This shows that the strength of the microwaves decreases with distance,
Place a metal plate between the transmitter and the receiver to show that microwaves cannot pass through metal.
Use to metal plates to make a narrow slit and show that the receiver detects microwaves that have been diffracted as they pass through the slit.
Show that if the slit is made wider, diffraction occurs less.
Use a narrower metal plate with the two plates from before to make a pair of slits and use the receiver to test for points of cancellation and reinforcement, where the microwaves from the two slits overlap.

4.5 STATIONARY AND PROGRESSIVE WAVES

Formation of stationary waves

When a guitar string is plucked, the sound produced depends upon the way the string is plucked.
If the string is plucked gently at the centre of the string, a stationary wave of constant frequency is created on the string.
If the string is plucked more vigorously, the string vibrates in a more complicated way and the note produced contains other frequencies, as well as the the frequency produced when the string is plucked gently.
A stationary wave is formed when two progressive waves pass through each other, this can be achieved on a string in tension by fixing both ends and plucking the middle, therefore the progressive wave travels towards each end, reflect at the end and then pass through each other.

The simplest stationary wave pattern as shown below, consists of a point of no displacement at both ends, called nodes and a point of maximum amplitude midway between the adjacent nodes, called anti nodes.
This is called the first harmonic on a string.

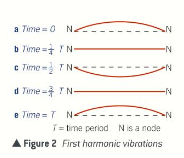
Distance between adjacent nodes= ½λ

If the frequency of the waves along the ropes from either end is raised steadily, the pattern from the previous diagram disappears and a new pattern is observed with two equal loops along the rope.
Frequency is double that of the first figure, but now half the wavelength.
This is because the distance from one node to another is = half a wavelength.
Length of the rope is equal to one full wavelength

Stationary waves that vibrate freely do not transfer energy to their surroundings.

Amplitude= 0 at nodes, therefore no energy at the nodes
Amplitude= maximum at the anti-nodes, so there is a maximum energy at the anti-nodes.
Because the nodes and anti-nodes are in fixed positions, no energy is transferred in a freely vibrating stationary wave pattern.

Explanation of stationary waves:

Considering a snapshot of two progressive waves passing through each other:

When they are in phase, they reinforce each other to produce a large wave as shown in this figure:
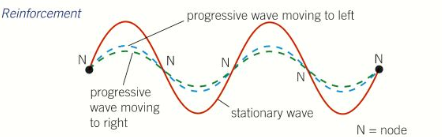
A ¼ of a cycle later, the two waves have each moved a quarter of a wavelength in opposite directions. They are in anti-phase and so they cancel each other out, as shown below:
A further quarter of a cycle, the two waves are back in phase, the resultant is again a large wave as shown in the first diagram.

The points where there is no displacement (the nodes) are fixed in position throughout. Between these points, the stationary wave oscillates between the nodes.
In any stationary wave pattern:

The amplitude of a vibrating particle in a stationary wave pattern varies with positions from zero at a node to a maximum amplitude at an anti-node.
The phase difference between the two vibrating particles is:

Zero if the two particles are between adjacent nodes or separated by an even number of nodes.
180° or π radians if the two particles are separated by an odd number of nodes.

	Stationary waves	Progressive waves
Frequency	All particles expect those at the nodes vibrate at the same frequency.	All particles vibrate at the same frequency
Amplitude	Amplitude varies from zero (nodes) and a maximum. (anti-nodes)	Amplitude is the same for all particles
Phase difference between two particles	Equal to mπ, where m is the number of nodes between the two particles.	Equal => 2πd/λ, where d= distance apart and λ is the wavelength

More examples of stationary waves:

Sound in a pipe:

Sound resonates at certain frequencies in an air filled tube or pipe. In a pipe closed at one end, the resonant frequencies occur when there is an anti-node at the open end and a node at the other end.

Using microwaves:

Microwaves from a transmitter are directed normally at a metal plate, which reflects the waves back towards the transmitter.
When a detector is moved along the line between the transmitter and the metal plate, the detector signal is found to be zero (or at a minimum) at equally spaces positions along the line.
The reflected waves and the waves from the transmitter form a stationary wave pattern.
The positions where no signal is found are where the nodes occur, they are spaced at intervals of half a wavelength.