8.1 FORCE AND ACCELERATION:
Motion without force:
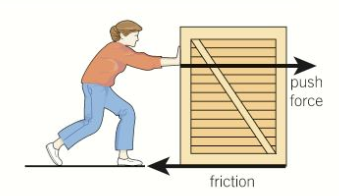
- On an icy road, drivers are careful due to the tires of cars having little to no grip.
- Moving from a standstill on ice is a challenge.
- Stopping on ice is almost impossible.
- Any pushing force is opposed by friction in the opposite direction to motion, provided that there exists a coefficient of friction.
Newton’s first law of motion:
Objects either stay at rest or moves with constant velocity unless acted on by a force.
- Newton was the first person to realise that a moving object remains in uniform motion unless an external force is acting on it.
- He recognised that when an object is acted on by a resultant force, the resultant force is to change the object’s velocity.
- An object moving at a constant velocity is either:
- Acted on by no forces.
- Forces acting upon it are balanced and therefore there is 0 resultant force.
Investigating force and motion:
- How does velocity of an object change if it is acted on by a constant force.
- The figure below shows how that can be investigated, with a dynamics trolley and a motion sensor connected to the computer.
- Computer is used to process a signal from the motion sensor.
- And therefore display a graph showing how the velocity of the trolley changes with time.
- Computer is used to process a signal from the motion sensor.
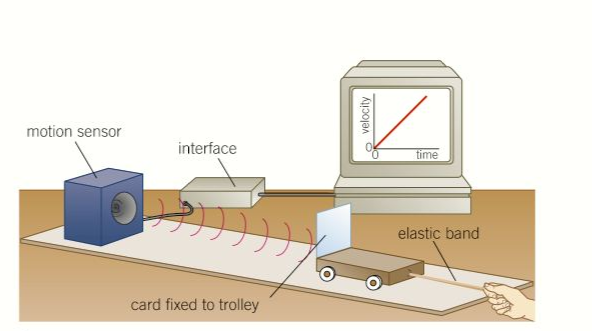
- Trolley is pulled along a sloping runway using one or more elastic bands stretched to the same length.
- The runway is sloped just enough to compensate for friction.
- As a result of pulling the trolley with a constant force, the velocity- time graph should show that the velocity increases at a constant rate.
- The acceleration is therefore constant and can be measured from the V-T graph.
- From this experiment, you can deduct that a force is proportional to mass × acceleration.
- F= ma
- The Newton is defined as the amount of force required to give an object of mass 1kg an acceleration of 1m/s2
- This equation is known as Newton’s second law for constant mass.
Weight:
- The acceleration of a falling object acted on by gravity is only g.
- The force of gravity is the only force acting upon the object, therefore it’s weight = mass × gravity.
- W=mg
- When an object is in equilibrium, the support force on it is equal and opposite to its weight.
- Therefore, an object placed on a weighing balance.
- Like a newton meter or a top pan balance.
- Exerts a force on the balance equal to the weight of the object.
- Therefore the balance measures the weight of the object.
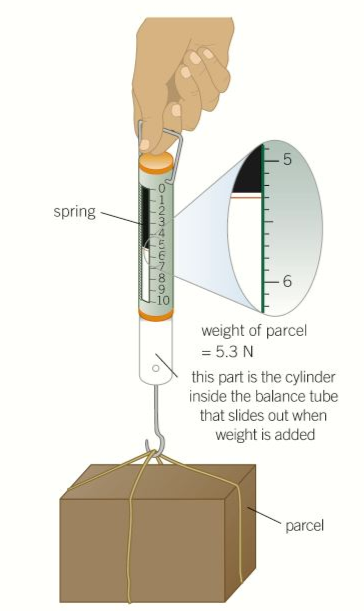
- Therefore, an object placed on a weighing balance.
- G is also referred to as the gravitational field strength at a given position.
- As it is the force of gravity per unit of mass
- g = 9.81m/s2
- Mass of an object is a measure of its inertia, which is the resistance to a change of motion.
- More force is needed to give an object a certain acceleration than to give an object with less mass the same acceleration.
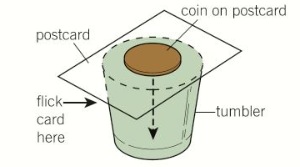
- A classic test for inertia is when a card is flicked, the coin drops into the glass because the force of friction on it due to the moving card is too small to shift it sideways, as shown in the diagram.
- Scale of a top pan balance is usually calibrated for convenience in grams or kilograms.
8.2 USING F=MA:
8.3 TERMINAL SPEED:
8.4 ON THE ROAD:
STOPPING DISTANCES:
- Most traffic accidents often occur because vehicles are being driven too fast and too close.
- A driver needs to maintain a safe distance between his or or her own vehicle and the vehicle ahead.
- If the vehicle ahead suddenly brakes, the driver of the following vehicle needs to brake as well to avoid the crashing into the car ahead.
Thinking distance:
- Is the distance travelled by a vehicle in the time it takes for the driver to react.
- For a vehicle moving at constant speed v, the thinking distance s1= speed ×reaction time = vt0, where the t0 is the reaction time.
- Reaction time is affected by alcohol, distractions or mobile phones.
Braking distance:
- Is the distance travelled by a car in the time it takes to stop safely, from when the brakes are first applied.
- Assuming constant deceleration, a, to zero velocity from speed u, the braking distance, s2= u ²/2a
Stopping distance:
- Stopping distance +braking distance = ut0+u ²/2a
- Figure below, shows how thinking, braking and stopping distances vary with speed for a reaction time of 0.67 seconds and a deceleration of 6.75 m/s2.

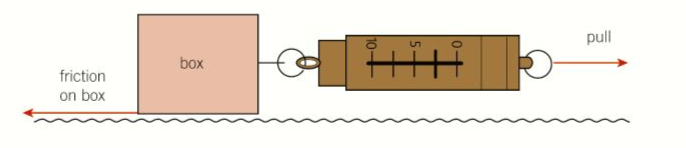
Practical, testing for friction:
- Measure the limiting friction between the underside of a block and the surface it is on.
- Pull the block with an increasing force until it slides.
- The limiting frictional force on the block is = to the pull force on the block.
8.5 VEHICLE SAFETY:
Measuring impacts:
- The effect of a collision on a vehicle can be measured in terms of the acceleration or deceleration of the vehicle.
- The force of an impact can be easily related to the weight of the vehicle.
- For example, a vehicle hits a wall at an acceleration of -30m/s2.
- In terms of g, the acceleration = -3g
- Therefore, the impact force of the wall on the vehicle must be three times its weight, therefore =3mg where m is the mass of the vehicle.
- The deceleration is 3g, not the impact force.
- A person sitting upright can only survive a deceleration of 20g for a few milliseconds.
- A deceleration of 5g for even a few seconds can cause fatal injuries.
Contact time and impact time:
- Impact time of t (duration of the impact force), can be worked out through the equation:
- S = ½(u+v)t: To one of the vehicles:
- s is the distance moved by that vehicle during impact.
- u being initial velocity
- v being final velocity
- If the vehicle mass is known, impact force can also be found out:
- For a vehicle of mass m, in time t:
- Impact time:
- t=2(distance)/(u+v)
- Acceleration:
- a= v-u/t
- Impact force:
- F=ma
Car safety features:
Vehicle bumpers:
- Give way a little in a low speed impact and so increase impact time, therefore impact force is reduced.
- If the initial speed of the impact is high, the bumper will likely be damaged.
Crumple zones:
- Engine compartment of a car is designed to give way in a front-end impact. If the engine compartment were rigid, the impact time would be very short, therefore the impact force would be very large.
- Designing the engine compartment to crumple, you an reduce impact force by increasing impact time.
Seat belts:
- A correctly fitted seat belt restrains the wearer from crashing into the vehicle frame after the vehicle suddenly stops.
- Restraining force on the wearer is much less than the impact force would be if the seat belt wasn’t there.
Collapsable sterring wheel:
- The seat belt restrains the driver without holding the driver rigidly.
- If the driver makes contact with the steering wheel, the impact force is lessened as a result of the collapse that occurs in the steering wheel.
Airbags:
- An airbag reduces force on the person, the airbag acts as a cushion and increases impact time on that person and therefore the impact force is spread over the contact area.
- Therefore the pressure on the body is less.
